There may never be another Einstein or another Newton, but we can all learn to utilize their equations under the right physical circumstances. We can become excellent at physics the same way they did: by solving problems.
KEY TAKEAWAYS
When most people think of a great physicist, they think of Einstein, often alongside his famous quote, "Imagination is more important than knowledge." Professional physicists, armchair physicists, and laypersons alike all have wild, imaginative ideas concerning how the world works, but very few ideas are worth serious scrutiny. This isn't because of bias, gatekeepting, close-mindedness, or dogmatism. It's because the expertise you gain in becoming a quality physicist teaches you how to separate out the nonsense.
All across the world, young adults are working hard toward making their dreams a reality. For many students at both the undergraduate and graduate levels, that dream involves unlocking the secrets of the Universe, taking us beyond our current understanding and beyond the Standard Models of both particle physics and cosmology. For generations, aspirational students have dreamed about becoming the next Heisenberg, Bohr, Dirac, Einstein, or even Newton, believing that they might have, inside their minds, the “secret sauce,” whatever it may be, to lead the next revolution in physics.
Most of them, unfortunately, wind up doing nothing of the sort. Revolutions in physics are extraordinarily hard to initiate, and for good reason: after centuries of theoretical and experimental work by thousands upon thousands of brilliant, competent minds, the current consensus models are strong and sturdy enough that they’re extraordinarily difficult to equal in terms of success, much less surpass. While numerous ideas abound, the critical evidence that would support any of them is sorely lacking. At the frontiers of physics, we’re all still stabbing in the dark.
But while the excellent physicists doing the stabbing are doing so with the equivalent of sharp knives, others have the equivalent of nerf bats, and don’t even realize the difference. In most cases, it’s because they never learned the secret to becoming an excellent physicist. Here’s the lesson they need to learn.
When most people think about breakthroughs in physics, they think about truly revolutionary ideas. They think about Einstein and his ideas — or thought experiments — that no one had conceived of before him.
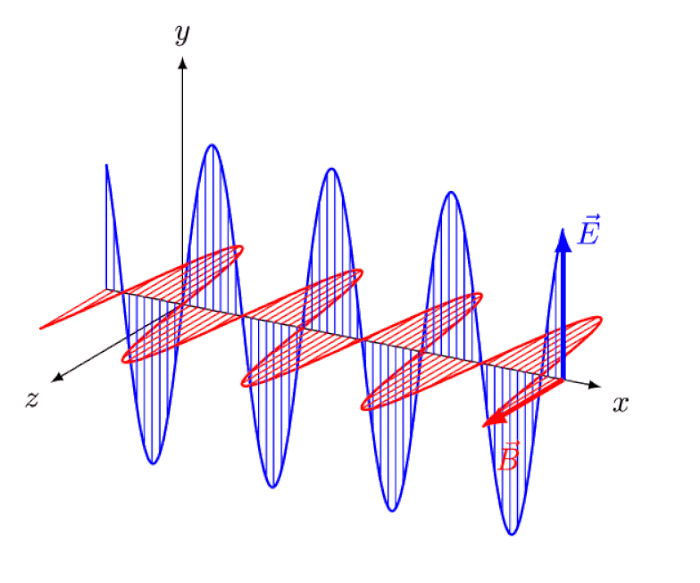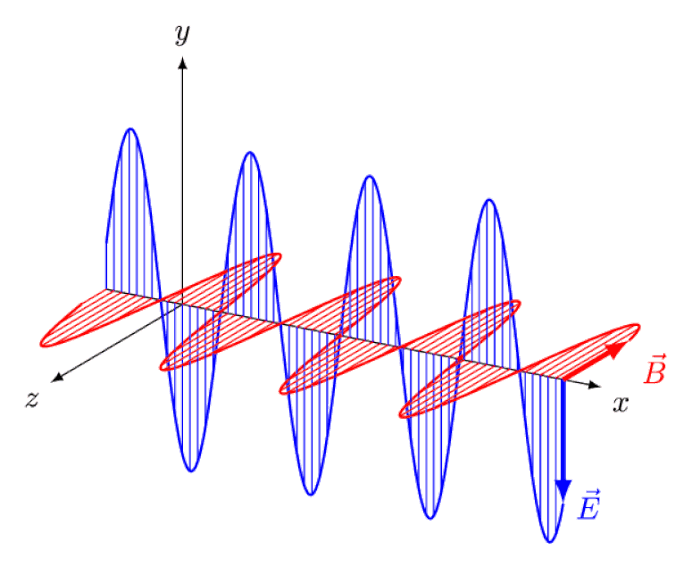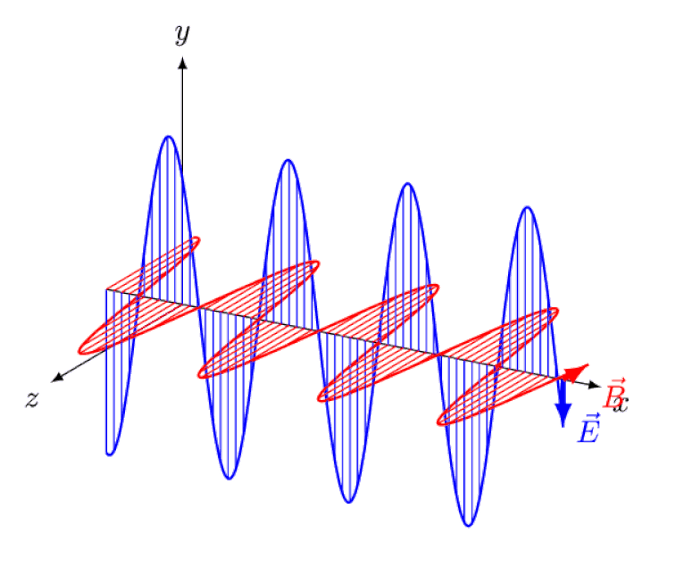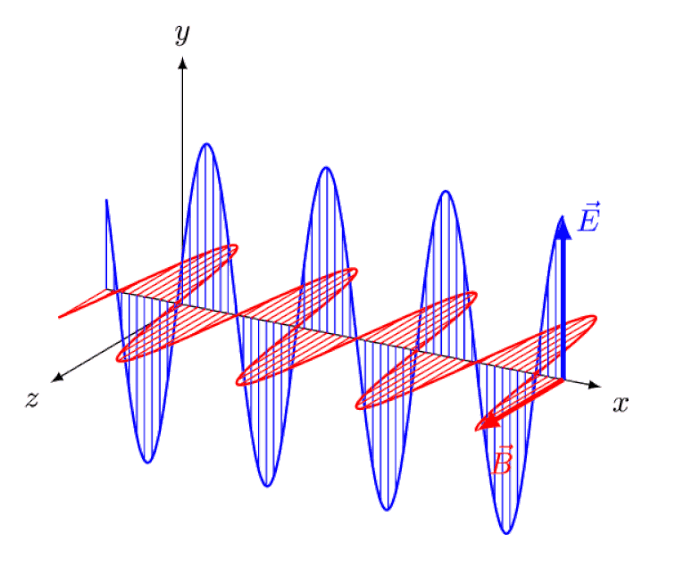
- They think about Einstein’s notion of “riding a light wave,” and what it would look like to see oscillating, in-phase electric and magnetic fields appearing and disappearing with a specific amplitude, and how no such phenomena exists: the thought-experiment that led him to the principle of relativity and the constancy of the speed of light.
- They think about the notion that, as objects move at speeds that take them closer to the speed of light, their kinetic energy increases dependent on your frame of reference, but in all frames of reference, a specific portion of that energy remains the same: enabling Einstein to derive the idea of a rest-mass energy and his most famous equation: E = mc².
- And they think about what Einstein himself called “his happiest thought,” or the notion that, from inside a closed room, you cannot tell whether you’re experiencing the downward pull of gravitation or the equal-and-opposite reaction from a constant thrust, or acceleration. This thought led to Einstein’s equivalence principle, which in turn eventually gave rise to Einstein’s General theory of Relativity.

It’s almost as if one person, even coming from outside the mainstream school of scientific thought, could almost single-handedly overturn the leading ideas in a modern scientific field and herald a revolution that leads us to a radical reconception of how the Universe works. Einstein himself seemed to agree with this notion, as you can find his famous quote, “Imagination is more important than knowledge,” practically anywhere you look.
But this fails to recognize the true extent of the background work that was necessary for Einstein to undertake, on his own, before any of these revolutionary thoughts could even begin to enter his head. It ignores the fact that Einstein went to school, learned physics, and even studied under one of the great mathematicians and physicists of his time: Hermann Minkowski. It ignores the fact that Einstein himself, even after leaving school, formed his own academy to study physics wherein he and his collaborators worked through the intricacies and consequences of various avenues of thought.
And it even ignores the context of Einstein’s full quote, which states,
“I am enough of an artist to draw freely upon my imagination. Imagination is more important than knowledge. For knowledge is limited, whereas imagination encircles the world.”

The key that most people miss about Einstein’s quote is that a certain level of knowledge — a level that eludes most people who don’t spend the necessary time and energy in gaining it — is required, as a prerequisite, to fully understand what our modern conception of the Universe is and isn’t successful at doing. That knowledge, of course, won’t lead you to any remarkable new insights on its own; for that, imagination is required as well, but it’s imagination that’s informed by a comprehensive foundational knowledge of where we are today and how we came to know the things that we actually meaningfully know.
Imagination is more important than knowledge as far as making novel advances go, in the sense that if you have two equivalent minds with equal knowledge of physics, but one is wildly imaginative and the other only limits their thoughts to what our current understanding has already revealed to us, the imaginative one is far more likely to blaze a revolutionary path forward than the one who has restricted their imagination. Great, novel ideas very rarely emerge from taking what is known and extrapolating to the next, minimally imaginative logical step. Imagination is required, and there’s no substitute for that key ingredient.

But while imagination is desirable for coming up with revolutionary ideas, a foundational knowledge of the physical theories and ideas that have led us to our current scientific consensus is absolutely mandatory. Many students — prior to beginning their undergraduate degree, while in pursuit of their bachelor’s degree, when considering graduate schools, or while a graduate student themselves — underestimate the importance of obtaining that knowledge, overestimate their reliance on their (not fully formed) physical intuition, and fail to recognize the critical step required to become an excellent physicist.
That key step?
It’s simplicity itself: you become good at physics by solving physics problems. That’s it: that’s the secret. If you want to become competent at physics, you will solve physics problems in the area you wish to learn.
Want to learn classical mechanics? Learn how to formulate the setup for a problem, write down the equations that describe the problem, work through the steps of solving those equations to arrive at physically relevant solutions, and use those solutions to work out the expected behavior of the system you’re considering.

Want to learn electromagnetism? Same thing: learn how to identify your knowns and unknowns, how to relate them through a series of equations and boundary conditions, how to solve that system of equations, and how to extract measurable and observable quantities that reveal your predicted answer.
It’s the same story with quantum mechanics, nuclear and particle physics, astrophysics, cosmology, geophysics, or any other physical system you dare to consider. You learn physics by solving problems; only through that specific avenue of exploring what physical consequences arise under certain specific conditions can you develop the intuition necessary to bring about an understanding of the kinds of physical systems you want to consider. This is true both experimentally and theoretically, as both classes of physics necessitate their own set of expertise and their own unique set of experiences in gaining it.
If you want to learn how to be a good swimmer, get in the water and swim. If you want to learn how to paint, get out the brushes and canvas and paint. If you want to learn how to play the piano, sit down in front of a piano and start playing those keys. And if you want to learn how to do physics, break out the problem sets or the experimental apparatuses and start solving physics problems.
That’s it. That’s the big secret: if you want to become competent at physics, you have to take on physics problems and become adept with the tools and techniques needed to solve them. In the history of physics, this has been a hallmark of absolutely everyone who’s made a meaningful contribution: either experimentally or theoretically or at the intersection of both. Without sufficient experience at problem solving, you simply cannot become a competent physicist, as only through the act of solving those key problems will you develop the necessary skills to become competent at this endeavor at all.
We all have gifts and talents, but one of the rude awakenings that many physics students receive at some point along their educational journey is that no matter your gifts and talents, there is no substitute for the development of necessary skills. Problem solving is something you can be talented at, for certain, but we all need practice at solving those problems in order to gain a competence and a familiarity — and to eventually develop an intuition that doesn’t lead you astray — when it comes to any particular area of physics. If you don’t put in that specific type of work, you’ll never develop the most important aspect of becoming good at physics: understanding the quantitative relationship between different physical phenomena and effects.
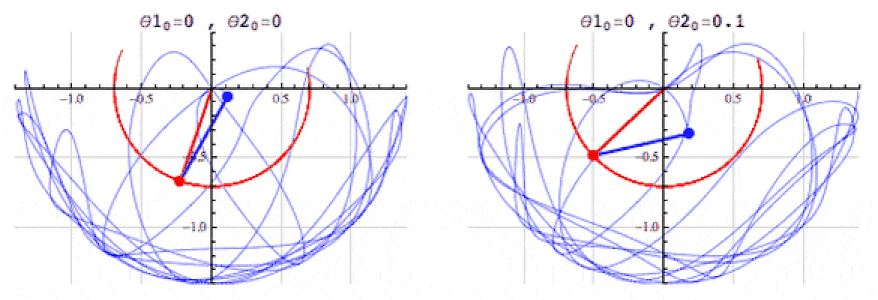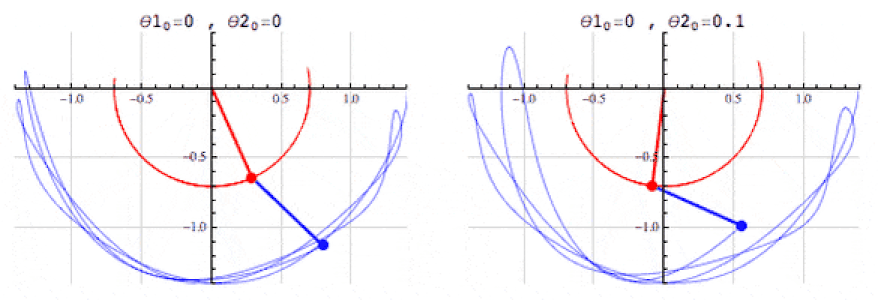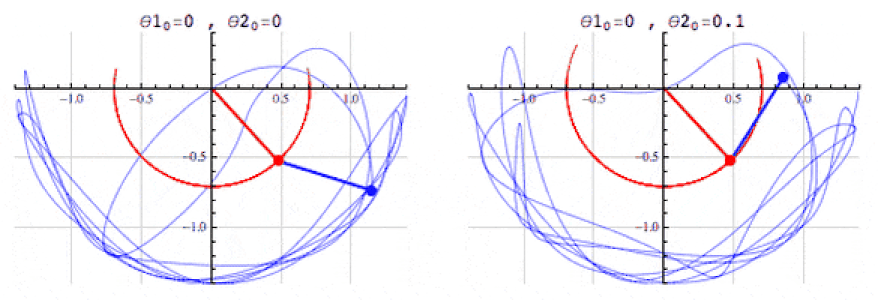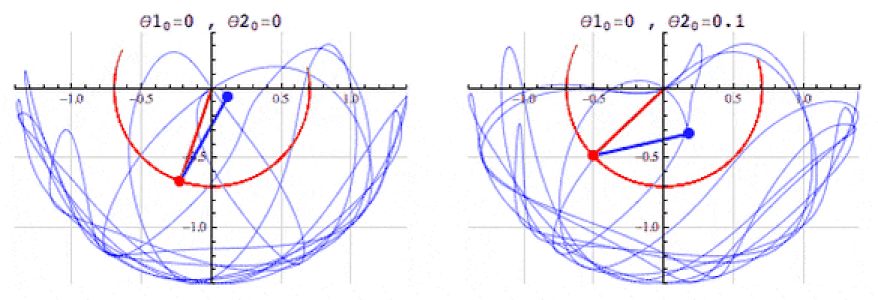
A lot of students are mystified at hearing this seemingly obvious advice, thinking they’re already following it as directed by attempting the assigned homework. Although you get partial credit for that, the main advice — you become good at physics by solving physics problems — has an important corollary: you need to learn a greater amount of physics than the physics you’d encounter simply from going through your assigned homework.
You need to learn the physics in your physics textbook, for example. Most students believe, erroneously, that if you read the textbook and refer to various sections of it, as needed, while solving your homework problems, that’s sufficient. Instead, I’d recommend the following course of action instead.
- Read the relevant section of the book before attending the lecture that will cover the material in the book, including taking notes and writing down the equations that appear.
- When you go to your lecture, take notes on everything the instructor writes down, including anything they say that you find relevant/interesting that they don’t write down.
- After your lecture — and before doing your homework — go through the relevant section of your book along with your lecture notes, and this time make sure you can step-by-step work through every problem that was solved and/or worked out in the lecture and in the relevant section of the book.
- And then, only then, after you’ve done all of that, should you go and do your homework.

If that sounds like a lot of work to put in, I’d encourage you to ask yourself this question: what do you hope to get out of an education in physics? Because all you’ll ever get out is directly proportional to the work you put in. The more time you spend with the equations, setting them up correctly under a variety of physical conditions, solving the relevant system of equations to find the unknown quantities based on what you can know/measure, and then comparing those predictions with something that’s measurable, the more capable you’ll be of correctly and usefully modeling a novel, newly considered system.
There are lots of other activities, many of which are worth the time and investment of effort, that can help you improve at physics in addition to setting up and solving relevant sets of problems.
- You can read books, including in-depth and popular accounts of various topics, often going back to the original sources where the idea you’re interested in was first put forth.
- You can read review papers and conference proceedings, which typically offer a broader, more modern, more accessible overview of a new field than a textbook or original source can.
- You can work through specialized textbooks, particularly ones that guide you through the equations relevant to the problems you’re considering.
But, once again, if you don’t work out the quantitative parts for yourself, you’re short-changing yourself on an intellectually fundamental level.
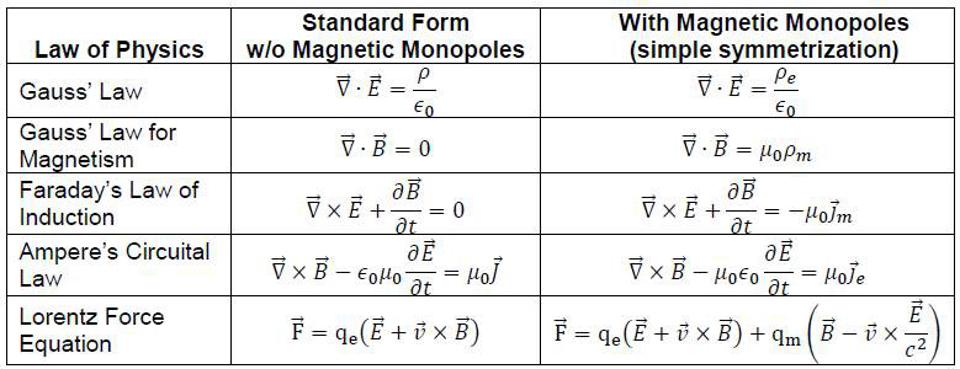
As a physicist, you’ll often receive solicitations from people who say things like, “I have an idea, I just need someone to help me with the math/details.” But unless you’re someone who’s worked through the quantitative details found in a variety of physical systems for yourself — likely correcting a vast array of misconceptions that you previously had before learning the lessons one learns by doing precisely that hard, quantitative work — you have no way of evaluating whether your idea even makes sense, much less if it has any merits.
You learn physics by solving problems, and by extension, if you haven’t solved the relevant problems, you almost certainly haven’t learned enough physics to be able to evaluate an idea in any sort of meaningful way. A huge part of learning physics involves disabusing yourself of notions that you possessed before you learned the valuable lessons one can only learn by doing that difficult, necessary, quantitative work to see which effects matter, and by how much, under a variety of circumstances. Imagination may be more important than knowledge, but a foundational level of knowledge is absolutely required for your imaginative thoughts to be relevant to the Universe at hand. You learn physics by solving problems, and that’s the secret key to achieving excellence in this particular scientific field.
Không có nhận xét nào:
Đăng nhận xét